Quantum Wave in a Box
Version: 1.0.2
Language: english
Developer: Michel Ramillon contact developer
© 2015-2017 Michel Ramillon
In Quantum Mechanics the one-dimensional Schrödinger equation is a fundamental academic and also exciting subject of study for both students and teachers of Physics. A solution of this differential equation represents the motion of a non-relativistic particle in a potential energy \(V(x)\). But very few solutions can be derived with just paper and pencil.
Quantum Wave in a Box
is a software for iPhone and iPad
designed to solve numerically
the one-dimensional Schrödinger equation
$$\quad i\frac { \partial }{ \partial t } \psi (x,t)\quad =\quad \underbrace { \left( -\frac { 1 }{ 2m } \frac { { \partial }^{ 2 } }{ { \partial x }^{ 2 } } \quad +\quad V(x) \right) }_{ H\quad operator } \quad \psi (x,t)\quad$$
$$in\quad atomic\quad units\quad (ħ = 1,\quad m_e=1,\quad e = 1)$$.
After input of the potential energy \(V(x)\) as an RPN expression, the software computes (for a potential with no imaginary part) eigenvalues and eigenfunctions of the hamiltonian operator H. A finite elements method is used for the spatial variable x over the interval representing the Box, while time remains a continuous variable.
The time-independent Schrödinger equation
$$H ψ(x) = E ψ(x)$$
represented by a set of linear equations, is solved using quick diagonalization routines. The solution \(ψ(x,t)\) of the time-dependent Schrödinger equation is then computed in matrix form as
$$ψ(x,t) = e^{-iHt} ψ_{0}(x)$$
where
$$ψ_{0}(x) = \left(\frac{1}{2 \pi \alpha}\right)^{\frac{1}{4}}e^{\frac{-{\left(x-x_{0}\right)}^{2}}{4 \alpha}}e^{ik_{0}\left(x-x_{0}\right)}$$
is a gaussian wave-packet at initial time \(t = 0\). Parameter \(x_{0}\) is the center of the wave-packet, \(\alpha = \sigma^{2}\) is related to the standard deviation \(\sigma\) and \(k_{0} = mv_{0}\) is the wave-vector.
Evolution in time of a gaussian wave-packet can be watched in animation for a large range of initial parameters.
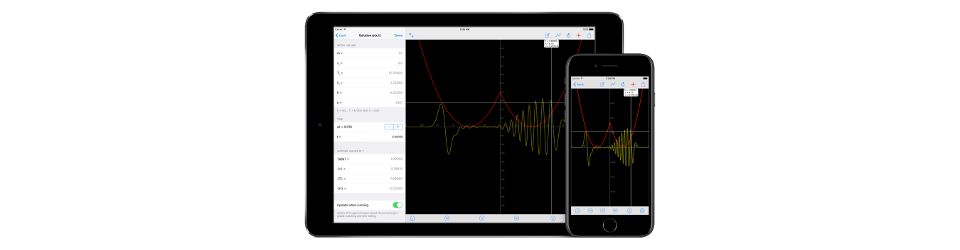
Examples of animations running on iPad for various potentials V(x)
In the animations below, the yellow curve represents the real part of the solution ψ(x,t) of Schrödinger’s equation, the white curve represents the density of probability of presence|ψ|² and the blue curve the free wave calculated from its exact analytical formula. The red curve stands for the potential energy V(x).
Available for iPad and iPhone on the App Store
- Atomic units used throughout (mass of electron = 1)
- Quantum system defined by mass, interval [a, b] representing the Box and (real) potential energy V(x).
- Spatially continuous problem discretized over [a, b] and time-independent Schrödinger equation represented by a system of N+1 linear equations using a 3, 5 or 7 point stencil; N being the number of x-steps. Maximum value of N depends on device’s RAM: up to 4000 when computing eigenvalues and eigenvectors, up to 8000 when computing eigenvalues only.
- Diagonalization of hamiltonian matrix H gives eigenvalues and eigenfunctions. If computing eigenvalues only, lowest energy levels of bound states (if any) with up to 10-digit precision.
- Listing of energy levels and visualisation of eigenwave-functions.
- Animation displays gaussian wave-packet ψ(x,t) evolving with real-time evaluation of average velocity, kinetic energy and total energy.
- Toggle between clockwise and counterclockwise evolution of ψ(x,t).
- Watch Real ψ, Imag ψ or probability density |ψ|².
- Change initial gaussian parameters of the wave-packet (position, group velocity, standard deviation), enter any time value, then tap refresh button to observe changes in curves without new diagonalization. This is particularly useful to get a solution for any time value t when animation is slower in cases where N is large.
- Watch both solution ψ(x,t) and free wave-packet curves evolve together in time and separate when entering non-zero potential energy region.
- Zoom in and out of any part of the curves and watch how ψ(x,t) evolves locally.
Privacy Policy
We as developer of the Quantum Wave in a Box App have absolutely no access to the user’s personal data during the installation or the use of the App. January 8th, 2023.